https://www.finmag.cz/firemni-kultura/326500-chces-svetovy-mir-porid-si-kamarady
Chceš světový mír? Pořiď si kamarády
Matematické modely naznačují, že spolupracující společnost se vyvíjí tam, kde nejprve existují malé skupiny spolupracujících jedinců s pevnými vazbami.

Historie lidstva je příběhem výjimečné spolupráce, ale také příběhem strašných konfliktů. Společnými silami jsme budovali města, civilizace a kultury – a také jsme je bořili při násilnostech jednoho vůči druhému, ničením životního prostředí… Když tedy víme, že v lidské přirozenosti je místo pro oba extrémy, mohli bychom nastavit parametry společnosti tak, aby se ke slovu dostávala spíš ta lepší stránka?
Ta otázka mimochodem není omezena na člověka. Příroda se doslova hemží všemožnými formami spolupráce, od mikrobů, kteří se dělí o prospěšné molekuly, po delfíny, kteří pomáhají svým raněným. Altruismus – sklon pomáhat druhým na vlastní úkor – je z pohledu evolučních vědců hádankou. Charles Darwin ve své knize O původu člověka napsal: „Kdo byl ochoten raději položit vlastní život [...], než aby zradil své soukmenovce, málokdy po sobě zanechal potomky, kteří by jeho šlechetnou povahu zdědili.“ Otázka pak zní, jaké podmínky vedou k evoluci kooperativního chování? Neplyne snad z principu přirozeného výběru, že sobeckost má vždy navrch?
Teorie o evoluci a lidském charakteru je obtížné testovat v laboratoři. Světlo do problému může přijít i ze směru, za jakého bychom ho nečekali: od matematiky. Myšlenka je: co kdybychom sestavili matematický model, jakýsi náčrtek reality z čísel a rovnic? Pomocí matematické analýzy bychom pak mohli snadno a rychle testovat věrohodnost evolučních hypotéz.
A přece pomůžeme!
Každý matematický model samozřejmě některé faktory pomíjí a jiné příliš zjednodušuje, takže si musíme dávat pozor, abychom z něj nevyvozovali příliš dalekosáhlé závěry. Historie je posetá troskami utopických idejí, které na papíře vypadaly skvěle, ale v praxi se zhroutily. Matematické modelování ale může být užitečné, i kdyby jen proto, že občas dokáže oddělit slibné nápady od těch z podstaty defektních.
Osobně jsem nedávno vedl výzkumný tým, který se pokusil pomocí matematických modelů zodpovědět otázku, jak společnost podporuje nebo naopak potlačuje evoluci kooperativního chování. Společenskou strukturu jsme znázornili jako síť, kde každý jedinec má nějaké „sousedy“. Vzájemné vztahy mohou být silné, například mezi blízkými přáteli či rodinnými příslušníky, nebo slabé, například mezi známými, kteří se často nevidí.
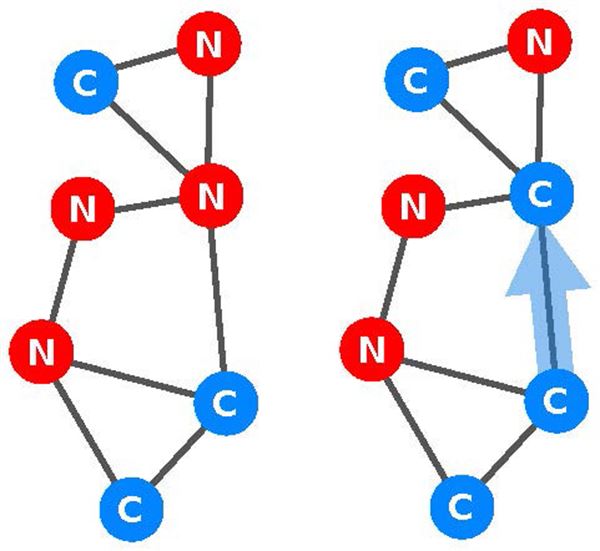
Jak se obě strategie – spolupráce (C) a nespolupráce (N) – šíří společenskou sítí podle toho, jak jednotliví participanti napodobují své sousedy.
Jedinci můžou buď spolupracovat, tedy pomáhat svým sousedům na vlastní úkor, nebo nespolupracovat. Tato volba je příkladem toho, čemu se v teorii her říká „vězňovo dilema“. Kdyby člověk jednal jen ve vlastním zájmu, druhým by nikdy nepomohl. A přesto – všeobecná spolupráce vede k vyšší životní úrovni všech zúčastněných.
Obě strategie – spolupráce a nespolupráce – se společenskou sítí šíří s tím, jak jedinci napodobují chování svých sousedů a učí se z něj. S větší pravděpodobností napodobují ty sousedy, kteří si vedou lépe v situacích typu vězňova dilematu. Časem jedna strategie zvítězí – společnost konverguje ke stavu, kdy spolupracují buď všichni, nebo nikdo.
V jakých sítích se šíří nákaza dobrem
Jedna starší studie zkoumala jednoduchou verzi tohoto modelu, v níž každý jednotlivec měl stejný počet sousedů. Vědci zjistili, že má-li spolupráce vzkvétat, musí být poměr jejího užitku a nákladů vyšší než počet sousedů na jednotlivce. Například pokud mají všichni pět sousedů, spolupráce se prosadí, získá-li z ní jednotlivec alespoň pětkrát vyšší užitek, než co do ní vloží. Výsledek je to sice velmi zajímavý, má ale jen omezenou praktickou využitelnost. V reálném světě sestávají společenské sítě z velmi rozdílných počtů sousedů – někdo jich má jen málo, jiní spoustu.
My v rámci svého pokusu přišli na způsob, jak vypočítat výhodnost spolupráce v libovolné síti. Klíčovou proměnnou je tu kritický poměr užitku a nákladů. Pokud činí například tři, pak je preferována spolupráce nabízející alespoň trojnásobný užitek. Ukázali jsme, jak vypočítat kritický poměr užitku a nákladů v libovolné síti pomocí soustavy lineárních rovnic, což je vcelku přímočarý matematicky úkon. Čím nižší poměr, tím snáze se rozšíří spolupráce. V některých sítích je ale kritický poměr záporný, což znamená, že spolupráce se v nich zřejmě nikdy evolučně neprosadí.
Jaké sítě jsou tedy k rozvoji spolupráce nejpříznivější? Spolupráce nejvíc kvete tam, kde má každý jedinec silné a opětované vzájemné vztahy s malým počtem sousedů. V takovém případě se spolupráce šíří lokálně, podél těchto linií, z čehož časem vzniká seskupení vzájemně spolupracujících jedinců, kteří sdílejí společný prospěch. Pokud jsou ale jednotliví aktéři spojeni se všemi ostatními v síti stejně silnými vztahy, prospěch ze spolupráce se rozředí v oceánu nekooperativních účastníků a kooperativní chování se nerozšíří. Jinými slovy – pro spolupráci je lepší hrstka silných vazeb než celá náruč slabých.
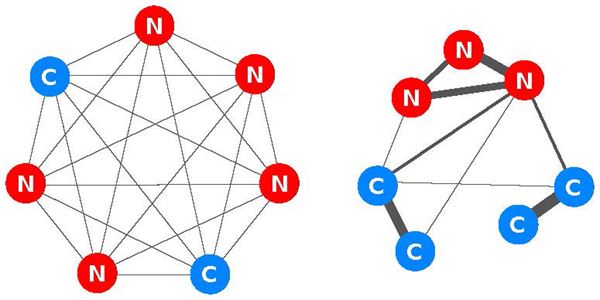
Když je každý propojený s každým stejně silnou vazbou, spolupracující jsou v nevýhodě. Pokud ale jednotlivci mají silné vazby jen na několik dalších, spolupráce vytvoří lokální hnízda vzájemné výpomoci, ze kterých pak může „zachvátit“ celou síť.
Lidstvo dnes čelí celé řadě bezprecedentních problémů. Boj s globálním oteplováním se neobejde bez spolupráce na celosvětové úrovni. Matematické modelování nám může pomoci s vytvářením struktur a institucí, které takovou spolupráci umožní. Vyjdeme-li z našeho modelu, pak otevřená fóra typu Twitteru se sice znamenitě hodí ke sdílení informací, ale vzájemnou spolupráci v zájmu společného dobra mezi uživateli příliš nepěstují. Instituce, které podporují menší počet silných vazeb, se možná k tomu účelu hodí lépe.
Tento práce představuje jen kousek výzkumného programu, který se snaží přijít na to, jak struktury, sítě a vzorce interakcí podporují spolupráci v živočišné říši i lidských společnostech. Náš model obnáší řadu zjednodušujících předpokladů, které je třeba důkladně prověřit, než si uděláme závěr, do jaké míry jsou naše závěry obecně aplikovatelné. Čeká nás ještě spousta práce – u pracovního stolu, v počítači, v laboratoři a hlavně v terénu – než porozumíme tomu, jaké typy sítí se nejlépe hodí k řešení našich společných problémů. Přesto i náš jednoduchý, abstraktní model naznačuje, že ten základní princip je pozoruhodně intuitivní – úspěch globální spolupráce závisí na síle lokálních vazeb.
Z anglického originálu Global cooperation depends on the strength of local connections, publikovaného na Aeon.com, pro Finmag přeložil Aleš Drobek
Nejnovější podcasty












