https://www.finmag.cz/finance/304178-soumrak-ornamentu
Soumrak ornamentů
Před nedávnem zde Pavel Kohout velmi trefně nazval podstatnou část rovnic moderní ekonometrie „matematickými ornamenty“. Nemohu souhlasit více. Přesto se domnívám, že matematika hraje v moderní ekonomii podstatnou roli: používá se k zastrašování nepřátel.

Když někdo nesouhlasí s vaší oblíbenou doktrínou (která je typicky zcela iracionální a často škodlivá), zahrňte ho rovnicemi. Nejen že tím vzbudíte zdání racionality, ale oponenti slabší povahy pokrčí rameny, zastydí se, že neznají jména příslušných ornamentů – a přestanou argumentovat. Přesto však má smysl pochopit, proč je velká část současné ekonometrie tak pomýlená. Jde totiž o velmi poučné nedorozumění.
Nejmíň je nejvíc
Přírodní vědy jsou pokusem o informační kompresi reálného světa v tom smyslu, že se snaží pomocí malého počtu základních principů vysvětlit a pochopit, co se ve skutečnosti děje. Jedním z takových základních principů je například koncept energie (mimochodem historicky velmi zajímavý, neboť energie není vidět, a tak chvíli trvalo, než na ni lidé začali věřit). Pomocí těchto konceptů konstruují přírodní vědy teorie o tom, jak (a v lepším případě i proč) svět funguje. Podstatné je, že každá taková teorie je formulována matematickým jazykem, typicky pomocí diferenciálních rovnic. Například zákon zachování hmotnosti formulovaný pro případ proudící tekutiny má tvar
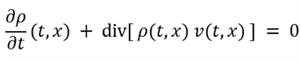
kde ρ(t,x) je hustota kapaliny nacházející se v čase t v bodě x a v(t,x) je rychlost kapaliny. Žádný ornament – v tomto případě jde o nejstručnější a nejpřesnější formulaci zákona, od kterého nejsou známy žádné odchylky.
Královna se zdobí
Humanitní vědy vždy pozorovaly snažení přírodovědců s blahosklonným nadhledem a nijak se jimi nenechaly vyvést z míry. Ve společenských vědách se však přírodovědná metoda – informační komprese formulované jazykem matematiky – stala předmětem nezřízeného obdivu a zdrojem trvalého minderwertigkeitskomplexu. A tak se začalo s ornamentním napodobováním matematického jazyka za usilovného doufání, že to společenským vědám přinese stejně fascinující úspěchy jako vědám přírodním. Toto počínání – v antropologii známé jakožto cargo cult – napáchalo asi největší škody v ekonomii, která se ráda nazývá královnou společenských věd.
Ironií osudu se s ornamentním užíváním matematiky v ekonomii začalo zrovna v době, kdy byla ve fyzice populární lineární rovnovážná termodynamika. To je obor, který zkoumá, jak se některé systémy (třeba sklenice se skotskou a ledem) vyvíjejí směrem k rovnováze (v našem případě sklenice s ředěnou skotskou). Lineární rovnovážná termodynamika je formulována matematickým jazykem, který formalizuje dva základní přírodní zákony: energie se vždy zachovává a entropie může jenom růst.
Vtom šli kolem ekonomové a hledali nějaký ornament, který vyšít na svou (veskrze náboženskou a estetickou) představu, že ekonomika by se měla také vyvíjet k nějaké rovnováze. Nebylo nic snazšího než prostě opsat rovnice lineární rovnovážné termodynamiky, jen místo hmotnost, tlak a teplota říkat třeba HDP, inflace a nezaměstnanost1. Už tehdy se objevily námitky, že neexistuje žádná analogie energie (veličina, která by se v ekonomice v čase zachovávala) ani entropie (veličina, která by v čase jen rostla)2. Celá lineární termodynamika je ovšem na těchto dvou principech založena. Není tedy žádný důvod, proč by její jazyk měl fungovat tam, kde oba tyto principy neplatí. Taky že nefunguje. Ale co by ekonom nedal za pěkný ornament. Dnešní DSGE modely jsou stále jen bohatými krajkami zdobené staré dobré rovnice lineární rovnovážné termodynamiky.
Co provedli ekonomové realitě
Fyzika mezitím urazila kus cesty a dnes začínáme aspoň trochu tušit, jak to chodí v systémech, které jsou daleko od rovnováhy. Chápeme, že takové systémy nemusejí směřovat k žádné rovnováze, mohou vykazovat chaotické (a tudíž principiálně nepředpověditelné) chování, probíhají v nich procesy samoorganizace, bývají náchylné ke skokovým změnám, následovaným obdobím relativního klidu a vůbec – mají se k lineárním systémům asi jako počítač k abakusu. Dodnes neexistuje žádná „teorie“ systémů daleko od rovnováhy a mnozí fyzikové věří, že nikdy žádná nebude. John von Neumann kdysi údajně přirovnal teorii nerovnovážných systémů k teorii ne-slonů.
Snaha popsat systém daleko od rovnováhy pomocí lineární teorie je předem odsouzena k nezdaru. Nabízím drobný příklad, abychom docenili, co všechno lze tupou linearisací ztratit. Vezmeme si nějaké číslo, umocníme je na druhou a k výsledku přičteme původní číslo. Celý postup opakujeme pořád dokola. Tvoříme tedy posloupnost
z, z2 + z, (z2 + z)2 + (z2 + z), a tak dále
Některá čísla (třeba z = 2) způsobí, že posloupnost bude rychle utíkat k nekonečnu. Jiná čísla (třeba z = -0,5) naopak nedovolí posloupnosti opustit okolí nuly. Teď si tuhle hru zahrajeme s komplexními čísly. Obarvíme černě všechna komplexní čísla, pro která výše uvedená posloupnost neopustí okolí nuly. Světle naopak obarvíme ta čísla, z nichž posloupnost uteče k nekonečnu. Výsledkem bude tato fascinující struktura známá jako Mandelbrotova množina.3
Dopřejte si psychedelický zážitek a na tomto videu se nechte provést nekonečným bohatstvím její struktury.
A teď pojďme Mandelbrotově množině udělat to, co udělali ekonomové realitě: linearizujme ji. Linearizací funkce f(z) = z2 + z kolem počátku dostaneme funkci g(z) = z. S touto novou funkcí si můžeme znovu zahrát starou Mandelbrotovu hru. Výsledkem bude tohle:4
Všechna ta fascinující nekonečně bohatá struktura je pryč! Zbyla jen černočerná tma. Na tyhle dva obrázky si prosím vzpomeňte vždycky, když vám bude nějaký ekonom něco vyprávět o modelech.
1 „Počkejte, počkejte, vejce, slanina a pivo? Já tady čtu Čechy, Morava a Slezsko!“ (Císařův pekař)
2 Dobrým kandidátem na analogii entropie by ovšem mohla být lidská blbost.
3 Mandelbrotova množina. Obrázek licencovaný jako CC BY-SA 3.0 vypůjčený od WikiMedia Commons. Čím světlejší barva, tím pomalejší konvergence k nekonečnu.
4 Obrázek vyrobil autor exkluzivně pro Finmag, není chráněn copyrightem, zdrojový kód k dispozici v redakci
Nejnovější podcasty

















