https://www.finmag.cz/finance/266516-fetis-cisel-jak-nemerit-nerovnost
Fetiš čísel: Jak neměřit nerovnost
Co je spočítáno, to je dáno, čísla nelžou. Proto se k nim často upínáme a jsme vcelku ochotní nadřadit je své intuici a „vlastním očím“. Takovým posvátným ukazatelem je třeba HDP. Jiným je Giniho index, ukazatel nerovnosti ve společnosti. Co je spočítáno, to je dáno – jenže, co když počítáme něco jiného, než si myslíme, nebo spočítané špatně interpretujeme? Pak jsme nahraní.

Evropou obchází strašidlo – strašidlo nerovnosti. A dorazilo i do Ameriky. Nerovnost je zde jedním z hlavních předvolebních témat. Barack Obama tvrdí, že celý problém Ameriky je, že bohatí nechtějí platit svůj spravedlivý díl do společné pokladny. Mává statistikami, že horní jedno procento Američanů zbohatlo za posledních třicet let o víc než 150 procent, zatímco dolních dvacet procent nezbohatlo vůbec. A má pravdu. Naopak Romneyho tábor tvrdí, že ani kdyby všichni Američani zaplatili na daních dvakrát tolik co loni, zdaleka to nebude stačit na všechny sliby a plány, které Obama má. Navíc poukazují na to, že téměř polovinu všech federálních daní z příjmů zaplatí horních deset procent Američanů, což je daleko víc, než je ve vyspělém světě běžné. V Německu činí tento podíl necelou třetinu, ve Švýcarsku dokonce jen pětinu a v Mekce zastánců rovnosti – Švédsku – asi čtvrtinu. Romney má taky pravdu. A pak se v tom vyznejte.
Každopádně obě strany zde (a všechny strany v Evropě) mávají Giniho indexem, který nerovnost ve společnosti měří. Vždy, když se místo nějakého stavu společnosti (například prosperity či rovnosti) začne cílovat jakýsi jeho kvantitativní ukazatel (v tomto případě HDP nebo Giniho index), je potřeba zbystřit. O neblahých důsledcích tohoto bláhového počínání jsem psal například tady.
Giniho index nerovnosti
Podívejme se tedy blíže na tento index, který Corrado Gini vymyslel ve volném čase, když zrovna nebásnil o vědeckém základě fašismu. Máme nějaký datový soubor, třeba celkový roční příjem tisíce různých lidí, a chceme nějak kvantifikovat variabilitu (nerovnost) v tomto souboru. Chceme to udělat tak, aby nerovnost byla nulová, pokud mají všichni stejný příjem, a maximální (rovná jedné) pokud jeden člověk má všechno a ostatní vůbec nic. Seřadíme tedy lidi podle výše jejich příjmů a podíváme se, jakou část celkových příjmů vlastní deset nejchudších lidí, dvacet nejchudších, třicet nejchudších, a tak dále. Když vyneseme tuto část celkových příjmů proti zlomku (majetkově seřazené) populace, která ji vlastní, dostaneme něco, čemu se říká Lorenzova křivka.
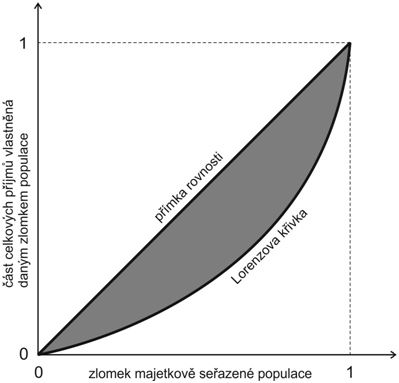
Kdyby měli všichni stejný příjem, Lorenzova křivka by byla rovná diagonála. Relativní prohnutí Lorenzovy křivky vzhledem k „přímce rovnosti“ se nazývá Giniho index. Spočítáme ho tak, že šedou plochu na obrázku vydělíme plochou trojúhelníku pod přímkou rovnosti. Protože plocha trojúhelníku je jedna polovina, je Giniho index roven dvojnásobku šedé plochy. Giniho index lze rovněž interpretovat jako střední (očekávanou) hodnotu relativního (tedy vztaženého k průměru souboru) rozdílu v příjmech mezi dvěma náhodně vybranými jedinci. To se líp chápe, ale hůř počítá.
Intenzita bohatství
Je jasné, že Giniho index skutečně nějak měří variabilitu v příjmech. Otázka je, jestli ji měří způsobem odpovídajícím našemu intuitivnímu chápání nerovnosti. To je dost důležité. Přijímáme-li totiž nějaké opatření, které vede ke snížení Giniho indexu (například 75% daň pro milionáře), většinou je nezamýšleným důsledkem tohoto opatření snížení střední hodnoty příjmů celé společnosti (milionáři budou méně pracovat nebo se odstěhují). Může se tedy stát, že kvůli stlačování jakéhosi čísla v konečném důsledku poškodíme všechny – chudé i bohaté.
Pokusím se to ilustrovat následující konstrukcí. Definuji jiný index nerovnosti a pokusím se vysvětlit, proč si myslím, že měří nerovnost přirozeněji. Potom se podívám, jak společnosti bohatnou a jak na to oba indexy nerovnosti reagují. Výsledky budou překvapivé.
Začněme definicí nového indexu nerovnosti. V mnoha případech člověk nevnímá přírodní děje skrze jejich absolutní (fyzikální) jednotky, ale skrze jakousi subjektivní stupnici, která lépe odpovídá našim „přijímačům“. Typickým příkladem je hlasitost zvuku. Nevnímáme absolutní intenzitu zvukového signálu (ve wattech na metr čtvereční), ale místo toho logaritmus podílu intenzity zvuku a intenzity nějakého prahového signálu (typicky zvuku na hranici slyšitelnosti). Takto je definován decibel. Tedy zvuk s tisíckrát větší (fyzikální) intenzitou bude vnímán jako o 30 decibelů hlasitější. A zvuk s milionkrát větší intensitou bude vnímán jako o dalších 30 decibelů hlasitější. Ucho tedy vykazuje něco, čemu ekonomové říkají „law of diminishing returns„ neboli zákon klesajících výnosů. Změna intenzity zvuku z jedničky na tisíc (tedy o 999 jednotek) přinese 30 decibelů. Na dalších 30 decibelů ale potřebuju změnu z tisíce na milion, tedy o 999 000 jednotek. „Decibelový výnos“ zvuku tedy prudce klesá s jeho rostoucí intenzitou.
Navrhuji, že bychom se měli dívat na bohatství podobným způsobem. Užitek, který mám z bohatství, totiž taky vykazuje klesající výnosy. Pokud mám stovku na den a vy máte tisícovku na den (rozdíl 900 korun), je to rozdíl mezi životem a smrtí. Pokud mám ovšem tisícovku na den a vy máte 1900 korun (stejný rozdíl), je to rozdíl mezi pohodlným životem a pohodlnějším životem. Proto si myslím, že je přirozenější bohatství měřit v „decibelech“ než v absolutních jednotkách. Definujme nějakou prahovou hodnotu B0, která bude odpovídat minimálnímu myslitelnému příjmu (hranice přežití, taková analogie hranici slyšitelnosti). Přepočítejme hodnotu bohatství ve společnosti podle vztahu
PB = log (B / B0),
kde PB znamená přepočtené bohatství a B je skutečné bohatství v korunách. Na tomto přepočteném bohatství potom spočítejme Giniho index a výsledku říkejme index LoGini, abychom připomněli, že jde o Giniho index na logaritmovaných datech.
Všichni bohatneme (bohužel jen pro příklad)
Představme si populaci tisíce lidí, ve které jsou nějak rozložené příjmy. Pro jednoduchost jsem příjmy vygeneroval z log-normálního rozdělení, což není nijak nerealistické (pro rýpaly dodávám, že jsem celý soubor posunul doprava o tisíc, aby se mi to lépe interpretovalo). Histogram bohatství tedy vypadá takto.
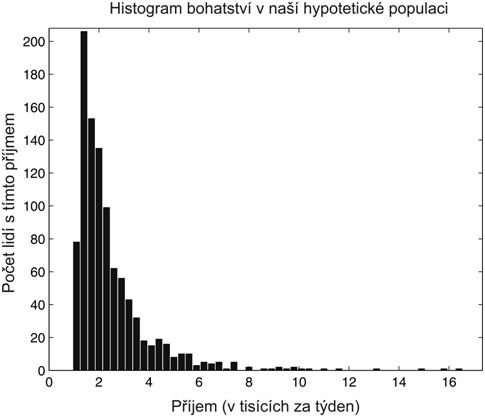
Podívejme se teď na tři scénáře bohatnutí společnosti. V prvním scénáři, nazvěme jej „Součet“, přidám každému člověku dva tisíce týdně. Tento způsob bohatnutí společnosti je velmi nerealistický a lze jej dosáhnout asi jen shazováním peněz z vrtulníku. Ve druhém scénáři, který nazveme „Násobek“ se zvýší každému příjem na dvojnásobek. To by odpovídalo situaci, že každý svůj příjem uloží do banky na stoprocentní úrok připsaný na konci týdne. Tento scénář je o dost blíže tomu, jak skutečná společnost bohatne (tedy pevným násobkem, nikoliv o pevnou částku), ačkoliv výše uvedená čísla by odpovídala snad jen Zimbabwe. Ve třetím scénáři, kterému říkám „Exponent“ udělám exponenciálu z příjmu každého jedince (přesněji řečeno, BNEW = 1000*exp (BOLD / 1000), abychom se neztratili v moři nul). Tento scénář odpovídá situaci, kdy je rychlost růstu příjmů úměrná velikosti těchto příjmů. To dává smysl, protože když máte milion, otevírá se vám škála daleko výnosnějších investičních možností, než když máte deset tisíc. Bohatí lidé mají tendenci bohatnout rychleji než chudí.
Prohlédněte si pečlivě následující graf:
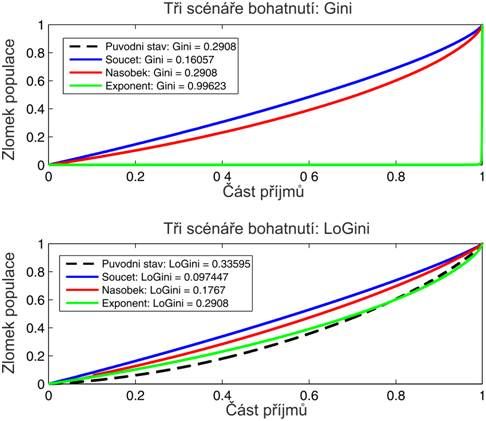
Předně si uvědomte, že ve všech třech scénářích celá společnost zbohatla, každý jednotlivec dostal přidáno. Při součtovém scénáři se střední hodnota i medián příjmů přibližně zdvojnásobily. Nerovnost měřená Giniho indexem pochopitelně klesla (původní černá křivka je překrytá červenou). Při násobkovém scénáři společnost jako celek zbohatla jen o něco víc než při součtovém scénáři. Giniho index zůstal přesně stejný, což je zřejmé z jeho konstrukce. Při exponenciálním scénáři se střední hodnota příjmů zvedla víc než milionkrát (což je samozřejmě dáno citlivostí střední hodnoty na extrémní pozorování) a medián se zvýšil skoro na čtyřnásobek. V tomto scénáři tedy společnost zbohatla daleko víc než v předchozích dvou. Giniho index ovšem vystřelil tak, že cílový stav je blízký absolutní nerovnosti (a zelená křivka na obrázku se plazí po dolním okraji grafu, než v poslední chvíli vystřelí k jedničce). Měli bychom tedy tendenci říct, že o takové bohatnutí společnosti nestojíme, protože vede k extrémní nerovnosti. Odmítneme tedy výrazné zvýšení příjmů pro všechny, protože jakési číslo se nebezpečně přiblížilo k jedničce.
Když všichni zbohatnou, budeme si rovnější!
Pokud ovšem měříme nerovnost indexem LoGini, vypadá najednou situace úplně jinak. Všechny tři scénáře bohatnutí vedou ke snížení nerovnosti! To je logické, protože jsme celou populaci vždy posunuli od nebezpečné hranice chudoby, kde jsou rozdíly smrtelně důležité, směrem vzhůru, kde jsou rozdíly méně závažné. Ve třetím scénáři se samozřejmě nerovnost snížila nejmíň, ale rozhodně bychom neměli tendenci jej kvůli tomu zamítnout.
Měli bychom si tedy rozmyslet, o co vlastně stojíme. Bohatnutí celé společnosti a snižování nerovnosti jsou procesy, které jdou často proti sobě (viz náš předchozí pokus o termodynamický popis tohoto fenoménu). Poměrně náhodné rozhodnutí, jakým indexem budeme měřit nerovnost (oba výše uvedené nápady dávají nějaký smysl) nás může dovést ke zcela opačným závěrům stran toho, co je žádoucí a co ne.
Ve skutečnosti je to ale s nerovností ještě úplně jinak. Lidé obecně nevnímají nerovnost skrze žádné indexy (domýšlivých akademiků), ale skrze svůj pocit, zda movitější spoluobčané dosáhli svého majetku více či méně úctyhodnými cestami. Společnost bývá poměrně vstřícná k lidem typu Henryho Forda, kteří svého závratného jmění dosáhli soukromým podnikáním, z nějž měla prospěch celá společnost. Akumulace majetku prostřednictvím rozkrádání veřejných zdrojů, podivných privatizací či sázek na cenu bankovních produktů (případnou prohru platí daňový poplatník) naopak žádný respekt nevzbuzuje. Dvě různé společnosti se stejným Giniho indexem můžou být svými občany vnímány jako málo nerovné (pokud bohatí nabyli majetku slušně) nebo naopak jako velmi nerovné (v případě opačném). Fyzikové tomu říkají path dependence.
Jaké z toho plyne poučení? Méně se soustředit na různé číselné ukazatele nerovnosti, u kterých není jasné, co a jak vlastně měří, a na kterých především zas tolik nezáleží. Víc se soustředit na to, aby se bohatství dosahovalo cestami, ze kterých má prospěch celá společnost.
Nejnovější podcasty















